समाधान और सहयोगात्मक गुण
परासरणी दवाब :
(मैं) $\quad \pi=\rho g$ कहाँ, $\rho=$ सोलन का घनत्व, $\mathrm{h}=$ संतुलन ऊंचाई.
(ii) वोंट-हॉफ फॉर्मूला (ओपी की गणना के लिए)
$\quad \quad \pi=\mathrm{CST}$
$\quad \quad \pi=\mathrm{CRT}=\frac{\mathrm{n}}{\mathrm{V}} \mathrm{RT}$ (बिल्कुल आदर्श गैस समीकरण की तरह)
$\quad \quad \therefore \mathrm{C}=$ कुल सांद्र सभी प्रकार के कणों का.
$\quad \quad = C_1 +C_2 +C_3 + \ldots \ldots \ $
$\quad \quad = \frac{(n_1 + n_2 +n_3 +\ldots\ldots)}{V}$
$If \quad V_1 mL \quad of \quad C_1 \quad conc.\quad + \quad V_2 mL\quad of\quad C_2 \quad conc.\quad are\quad mixed.$
$\quad\quad \pi = (\frac{C_1V_1 +C_2 V_2}{V_1 +V_2})RT;$
$\quad \quad \pi = (\frac{\pi_1V_1 +\pi_2 V_2}{RT});$
समाधान का प्रकार:
(ए) आइसोटोनिक समाधान - समान ओपी वाले दो समाधान
$\quad \quad\pi_{1}=\pi_{2} \text { (at same temp.) }$
(बी) हाइपर टॉनिक- यदि $\pi_{1}>\pi_{2} .\left.\Rightarrow\right|^{\text {st }}$ समाधान हाइपरटोनिक समाधान wrt है $2^{\text {nd }}$ समाधान।
(सी) हाइपोटोनिक - II ${ }^{\text {nd }}$ समाधान हाइपोटोनिक wrt प्रथम समाधान है।
**असामान्य सहसंयोजक गुण : (संबंध या पृथक्करण के मामले में) **
वांट हॉफ सुधार कारक (i) :
$\quad \quad i=\frac{\text { exp/observed / actual / abnormal value of colligative property }}{\text { Theoritical value of colligative property }}$
$\quad \quad =\frac{\text { exp./ observed no. of particles / conc. }}{\text { Theoritical no. of particles }}\quad =\frac{\text { observed molality }}{\text { Theoritical molality }}$
$\quad \quad =\frac{ \text{theoretical molar mass (formula mass)}}{\text{ experimental / observed molar mass (apparent molar mass)}}$
- $\mathrm{i}>1 \Rightarrow$ पृथक्करण.
$\quad \quad \mathrm{i}<1 \Rightarrow$ संगठन।
- $i =\frac{\pi_{exp.}}{\pi_{theor }}$
$\therefore \quad \pi =iCRT$
$ \quad \quad\pi =(i_{1} C_{1}+i_{2} C_{2}+i_{3} C_{3} \ldots . .){RT} $
i & के बीच संबंध $\alpha$ (पृथक्करण की डिग्री) :
$$ \mathrm{i}=1+(\mathrm{n}-1) \alpha \quad \text {कहाँ, } \mathrm{n}=\mathrm{x}+\mathrm{y} \text {. } $$
संबंध की डिग्री के आधार पर संबंध $\beta$ & $i$.
$$ i=1+\left(\frac{1}{n}-1\right) \beta $$
वाष्प दबाव में सापेक्ष कमी (आरएलवीपी):
भाप बल: $\mathrm{P}_{\text {Soln. }}<\mathrm{P}$
में कम करना $V P=P-P_{S}=\Delta P$
वाष्प दबाव में सापेक्ष कमी $R L V P=\frac{\Delta P}{P}$
राउल्ट का नियम: (गैर-वाष्पशील विलेय के लिए)
वीपी में प्रायोगिक तौर पर सापेक्ष कमी $=$ विलयन में अवाष्पशील विलेय का मोल अंश।
$$ RLVP=\frac{P-P_{s}}{P}=X_{\text {solute }}=\frac{n}{n+N} $$
$$ \frac{P-P_{s}}{P_{s}}=\frac{n}{N} $$
$$ \frac{P-P_{s}}{P_{s}}=(\text { मोललिटी }) \times \frac{M}{1000} \quad \quad ( M = \text{विलायक का दाढ़ द्रव्यमान}) $$
यदि विलेय संबद्ध या विघटित हो जाता है
$$ \शुरू{संरेखित} और \frac{P-P_{s}}{P_{s}}=\frac{i . n}{N} \\ और \frac{P-P_{s}}{P_{s}}=i \times(\text { molality }) \times \frac{M}{1000} \अंत{संरेखित} $$
राउल्ट के नियम के अनुसार
(मैं) $p_{1}=p_{1}^{0} X_{1}$. कहाँ $X_{1}$ विलायक (तरल) का मोल अंश है।
(ii) एक वैकल्पिक रूप $\rightarrow \frac{p_{1}^{0}-p_{1}}{p_{1}^{0}}=x_{2}$.
क्वथनांक में ऊंचाई:
$ \डेल्टा T_{b}=i \गुना K_{b}m$
$K_{b}=\frac{RT_{b}^{2}}{1000 \times L_{vap}} C \text { or } \quad K_{b}=\frac{RT_{b}^{2}M}{1000 \times \Delta H_{vap}}$
$L_{vap}=(\frac{\Delta H_{vap}}{M}) $
हिम बिंदु में अवनमन
$\therefore \Delta T_{f}=i \times K_{f} . m$.
$K_{f}=$ मोलल अवसाद स्थिरांक $=\frac{RT_f^{2}}{1000 \times L_{\text {फ्यूजन } }}$
$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad=\frac{RT_f^{2}M}{1000 \times \Delta H_{\text {फ्यूजन } }}$
वाष्पशील तरल पदार्थों के बाइनरी (आदर्श) मिश्रण के लिए राउल्ट का नियम:
$P_A = X_AP_A^{0} \quad \therefore P_B = X_B P_B^0$
$if\quad P_A^0 > P_B^0 \quad \therefore \quad A \quad is\quad more \quad volatile \quad than \quad B$
$\quad \quad \quad \quad \quad \quad\quad \therefore \quad$ ए का बी.पी $<$ का बी.पी $B$
$\quad \quad \quad \quad \quad \quad\quad\therefore \quad$ डाल्टन के नियम के अनुसार
$\quad \quad \quad\quad\quad \quad \quad P_T = P_A + P_B = X_AP_A^0 + X_BP_B^0$
$X_{A}{ }^{\prime}=$ का मोल अंश $A$ द्रव/समाधान के ऊपर वाष्प में।
$X_{B}{ }^{\prime}=$ का मोल अंश $B$
$ P_{A}=X_{A} P_{A}{ }^{0}=X_{A}{ }^{\ prime} P_{T}$
$P_{B}=X_{B}{ }^{\prime} P_{T}=X_{B} P_{B}{ }^{0}$
$\frac{1}{P_{T}}=\frac{X_{A} ^{\प्राइम}}{P_{B}{ }^{0}} . $
सचित्र प्रदर्शन :
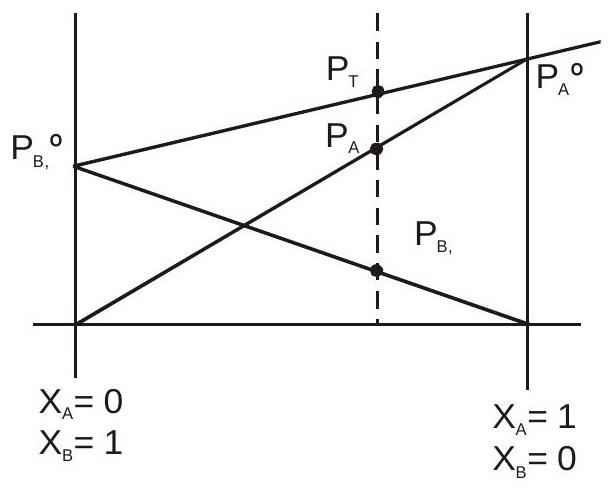
से भी अधिक अस्थिर $B\left(P_{A}{ }^{0}>P_{B}{ }^{\circ}\right)$
आदर्श समाधान (मिश्रण) :
मिश्रण जो सभी तापमान पर राउल के नियम का पालन करते हैं।
$\quad \quad A$ —— ए $\quad \Rightarrow \quad A$ —— $B$,
$\quad \quad$ बी ——– बी
$\quad \quad \Delta H_{mix}=0 \quad: \quad \Delta V_{mix}=0$
$\quad \quad \Delta S_{mix}=+$ आगे बढ़ने की प्रक्रिया के संबंध में: $\Delta G_{mix}=-ve$
जैसे. $\quad $(1) बेंजीन + टोल्यूनि।
$\quad \quad $ (2) हेक्सेन + हेप्टेन।
$\quad \quad$ (3) $C_2 H_5 Br + C_2 H_5 I$.
गैर-आदर्श समाधान: जो राउल्ट के नियम का पालन नहीं करते हैं।
(ए) सकारात्मक विचलन :-
(मैं)$P_{T,exp} > (X_AP_A^0 + X_BP_B^0)$
(ii)$\mathrm{A}-\mathrm{A}>\mathrm{A}–\mathrm{B}$
$B-B>A–B$
$\downarrow$
आकर्षण का बल
(iii) $\Delta \mathrm{H}_{\text {mix }}=+\mathrm{ve}$ ऊर्जा अवशोषित
(iv) $\Delta V_{mix}=+ve(1L+1L>2L)$
(वी) $\Delta \mathrm{S}_{\text {mix }}=+\mathrm{ve}$
(vi) $\Delta \mathrm{G}_{\text {mix }}=-\mathrm{ve}$
जैसे. $H_{2}O + CH_{3}OH$.
$H_{2}O + C_{2} H_{5} OH$
$C_{2} H_{5} OH + hexane$
$C_{2} H_{5} OH + cyclohexane$
$CHCI_3 + CCI_4 \rightarrow \text{dipole dipole interaction becomes weak}.$
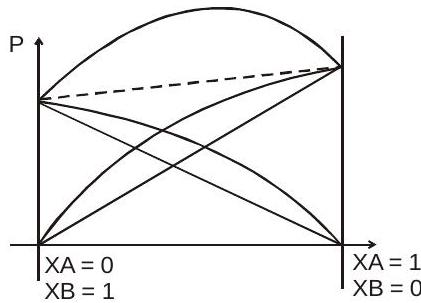
$P^{0}A > P{^0} B$
(बी) नकारात्मक विचलन
(मैं)$P_{T}exp < X_A P_A^{0} + X_B P_B^{0}$
(ii)$\mathrm{A} —- \mathrm{A}>\mathrm{A} —- \mathrm{B}$
$B —- B>A —- B$
आकर्षण बल की शक्ति.
(iii) $\Delta \mathrm{H}_{\text {mix }}=-\mathrm{ve}$
(iv)$\Delta \mathrm{V}_{\text {mix }}=-\mathrm{ve} \quad $ $(1L + 1L < 2L)$
(वी) $\Delta \mathrm{S}_{\text {mix }}=+\mathrm{ve}$
(vi) $\Delta \mathrm{G}_{\text {mix }}=-\mathrm{ve}$
जैसे. $H_2O + HCOOH$
$H_2O + CH_3COOH$
$H_2O + HNO_3$
$CHCI_3 + CH_3OCH_3$
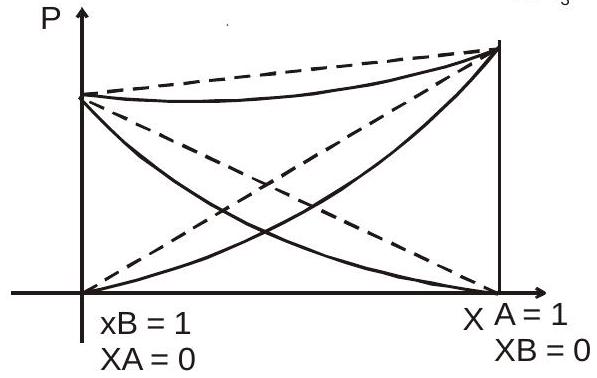
$P^{0}A > P{^0} B$
अमिश्रणीय तरल पदार्थ:
(मैं)$P_{\text {total }}=P_{A}+P_{B}$
(ii)$P_{A}=P_{A}^{0} X_{A}=P_{A}^{0} \quad\left[\right.$ तब से, $\left.X_{A}=1\right]$.
(iii)$P_{B}=P_{B}{ }^{0} X_{B}=P_{B}^{0} \quad\left[\right.$ तब से, $\left.X_{B}=1\right]$.
(iv)$P_{\text {total }}=P_{A}^{0}+P_{B}^{0}$
(वी)$\frac{P_{A}^{0}}{P_{B}^{0}}=\frac{n_{A}}{n_{B}}$
(vi)$\frac{P_{A}^{0}}{P_{B}^{0}}=\frac{W_{A} M_{B}}{M_{A} W_{B}}$
$P_{A}{ }^{0}=\frac{n_{A} R T}{V} ; \quad P_{B}{ }^{0}=\frac{n_{B} R T}{V}$
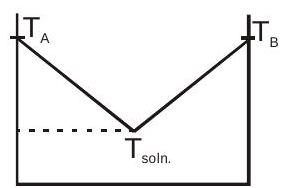
घोल का बीपी दोनों तरल पदार्थों के व्यक्तिगत बीपी से कम है।
हेनरी लॉ
यह नियम तरल में गैस के विघटन से संबंधित है अर्थात प्रति इकाई आयतन में किसी विलायक में घुली किसी भी गैस का द्रव्यमान तरल के साथ संतुलन में गैस के दबाव के समानुपाती होता है।
$m \propto p$
$\mathrm{m}=\mathrm{kp}$
$\mathrm{m} \rightarrow \frac{\text { weight of gas }}{\text { Volume of liquid }}$










